
Spanning Trees
A spanning tree of a graph,
G, is a set of |V|-1 edges that connect all vertices of the graph.
Minimum Spanning Tree
In general, it is possible to construct multiple spanning trees for a graph,
G. If a cost, Cij , is associated with each edge, Eij = (Vi,Vj), then the
minimum spanning tree is the set of edges, Espan, forming a spanning tree,
such that:
C = sum( Cij | all Eij in Espan)
is a minimum.
Minimum Spanning Trees : why do
need it?
often we require to interconnect a set of'n' piins with using least amount
of connecting material or at least cost of connection ,we can model such
problems with the a& Undirected Graph G=(V,E)V being the set of pins
and E being the set of edges connecting the pins,we wish to Suppose we
have a group of islands to find out a cyclic subset connecting all
vertices for which total weight is minimum that we wish to link with bridges
so that it is possible to travel from one island to any other in the group.
Further suppose that (as usual) our government wishes to spend the absolute
minimum amount on this project (because other factors like the cost of
using, maintaining, etc, these bridges will probably be the responsibility
of some future government ). The engineers are able to produce a cost for
a bridge linking each possible pair of islands. The set of bridges which
will enable one to travel from any island to any other at minimum capital
cost to the government is the minimum spanning tree.
There are two basic Algorithm regarding Minimum Spaning Tree ,Kruskal's
Algorithm and Prim's Algorithm,and
are elobration of 'generic algorithm' .
Kruskal's Algorithm
Kruskal's Algorithm is a Greedy Algorithm. It select light weight edge
one by one and checks if the corresponding edges are reachable by any path
made up of edges which already colored except that currently choosen
path ,if it gives negetive result, we color it make it a way for spanning
down the graph else the edge is left unchanged.
Algorithm :
MST_KRUSKAL(G,w)
1. A <--null
2. for each vertex v belonging V[G]
3.
do Make_Set(v)
4. sort the edges of E by non-decreasing weight w
5. for each edge (u,v) belonging to
E,in order by nondecreasing weight
6.
do if Find_Set(u)!=Find_set(v)
7.
then A<-A U {(u,v)}
8.
UNION(u,v);
9. return A
WORKING OF THE ALGORITHM
Lines 1-3
initialize the set A to the empty set and creates \V\ trees,one containing
each vertex. The Edge in E are sorted in non decreasing weight in Line
4.the for loop covers Line
5-8 ,checks
wether for Edge (u,v),wether the end points u and v are belonging
to same tree if yes they can't be added again otherwise it
is added in Line
7 and then the Vertices in two Trees are
merged in Line
8.
Analysis:
The run time of algorithm
is O(ElgE).the initialization O(V) time and time to sort the Edge is O(ElgE)
and finally O(E) time to find mutual independent search of vertices.
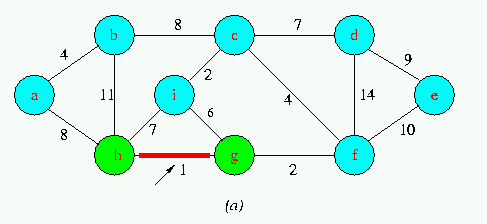
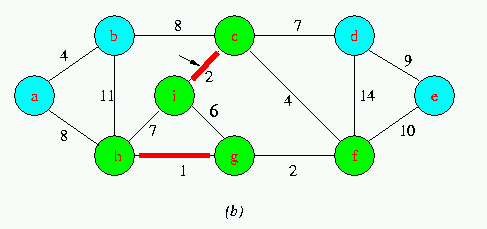
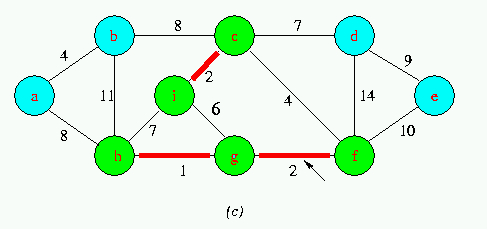
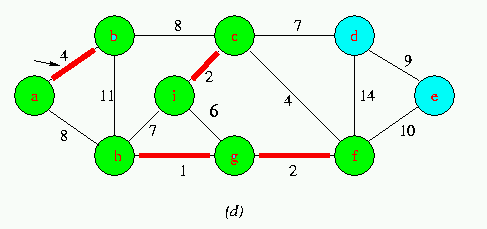
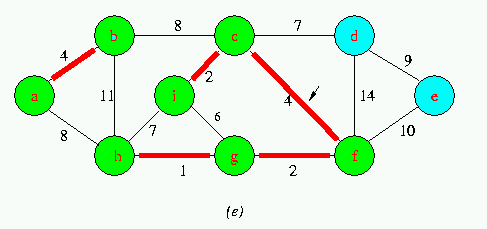
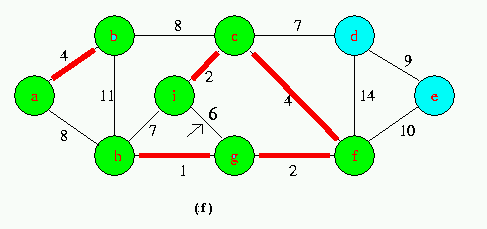
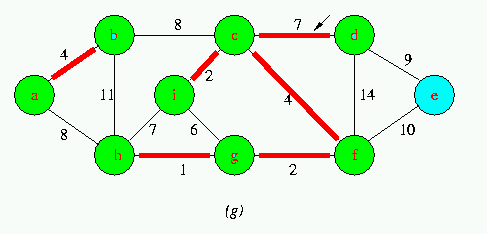
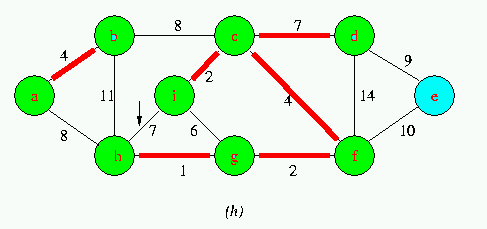
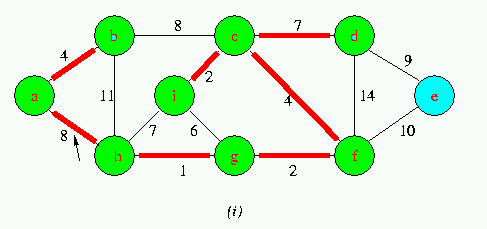
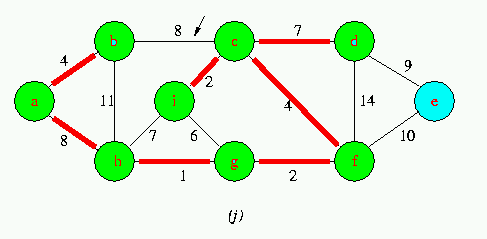
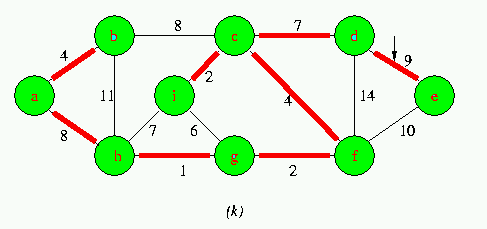
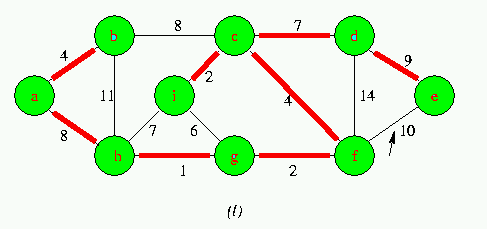
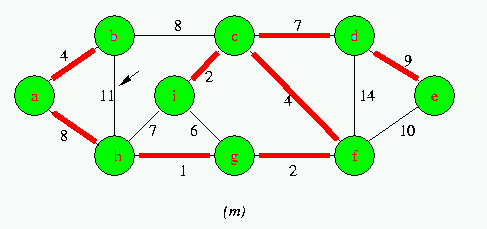
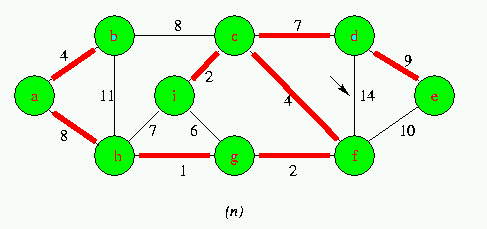
Execution of Kruskal's Algorithm on the graph
Red colored edges belong to the forest A being grown.The edges are considered by the algorithmis sorted order by weight.An arrow points to the edge under consideration at each step of the Algorithm If the edge joins two distinct trees in the forest,it is added to the forest,thereby merging the two trees.
Run Animation
Prim's Algorithm
Prim Algorithm works much like
Dijkstra's Algorithm and it has a special property that the vertices always
form a single tree.The tree starts from an arbitrary root vertex r and
grows until the tree spans all the vertices in V.At each step a light edge
connecting a vertex in A to a vertex in V-A is added to the tree .
Algorithm
1. Q <-- V[G]
2. for each u belonging to Q
3.
do key[u] <-- infinity
4. key[r] <-- 0
5. parent[r] <--NIL
6. while Q !=null
7.
do u <-- EXTRACT-MIN(Q)
8.
for each V belonging to Adj[u]
9.
do if V belong to Q and W(u,V)<key[v]
10.
then parent[V] <-- u
11.
key[V] <--W(u,V)
Working of Algorithm
Line 1-4
initialize the Priority Queue Q to contain all the vertices and set the
key of each vertex to infinity except for root which is set to 0,Line
5 initialize parent of root to NILL,Throughout
the Algorithm the set V-Q contains the vertices in the tree being grown.Line
7 indentifies a vertex u of set Q incident
on a light edge crossing the cut (V-Q,Q) .Removing u from the set Q adds
it to the set V-Q of the vertices in the tree. Line
8-11 updates the key and parent fields of
every vertex V adjacent to u but not in the tree.
Performance of the Prim's Algorithm is of the order
of ElgV
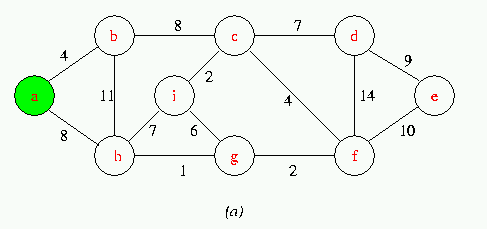
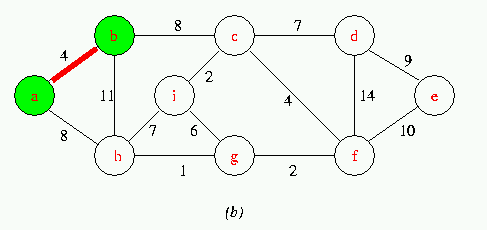
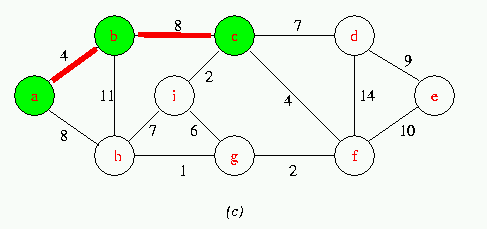
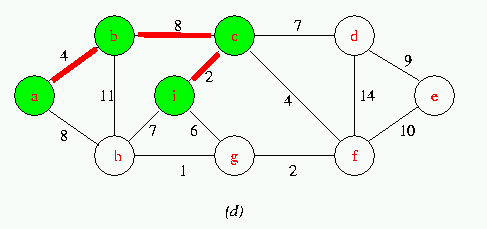
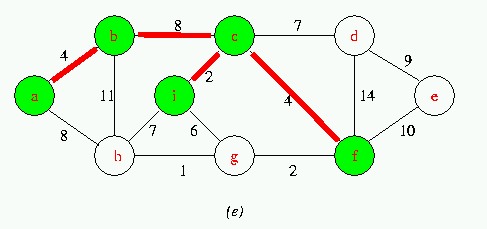
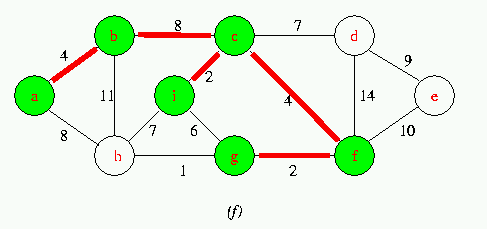
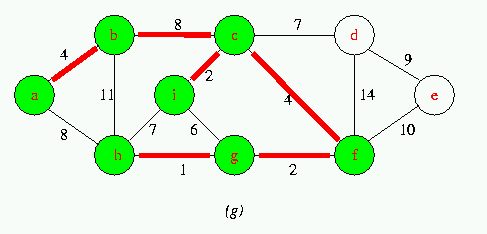
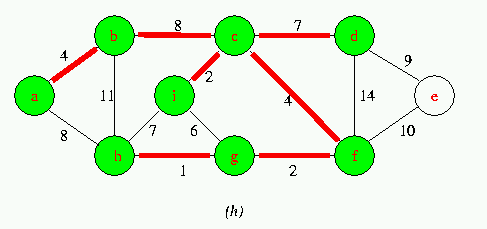
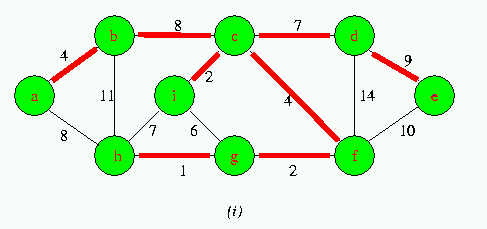
Execution of Prim's Algorithm on the graph
The root vertex is a. Red colored edges are in the tree being grown,and the vertices in the tree are shown in green .At each step of the Algorithm ,the vertices in the tree determine a cut of the graph ,and a light edge crossing the cut is added to the tree.
Run Animation


Key to Home
Minimum Spanning Tree
Graph Algorithms
This tutorial is written
by Abhishek Goyal,Marghoob Moyinoodin,Pooja Nath and Ruchi Saran |
Please email comments to:
[email protected][email protected] |
© Abhishek
Goyal
, 1999


























